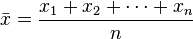This is the third post in our discussion of image segmentation. The first post talked about splitting an image by RGB color using ImageJ / Fiji. Then I talked about using k-means segmentation and the L*a*b color space. You might remember that I was pretty excited about the technique. Is it a general solution to all segmentation problems?
Let's try it on this image.
When I look at this picture, I see 3 colors: white, black/blue and lots of red. Let's convert from RGB to L*a*b and then split into 3 regions using k-means segmentation. The MATLAB code to do this is
function k_means_clustering
image_file_string = '3mokotri.tif';
% Load image
im_rgb = imread(image_file_string);
% Transform to lab color space
cform = makecform('srgb2lab');
im_lab = applycform(im_rgb,cform);
% Create a n x 2 matrix of [a b] values
a = im_lab(:,:,2);
a = double(a(:));
b = im_lab(:,:,3);
b = double(b(:));
ab = [a b];
% Construct the 2D histogram with appropriate limits
c{1}=[min(ab(:)) : max(ab(:))];
c{2}=c{1};
n = hist3(ab,c);
n1 = n';
n1(size(n,1) + 1, size(n,2) + 1) = 0;
% Display
figure(1);
clf;
imagesc(log10(n1));
hold on;
title('2D histogram of pixel values, colored based on log10 of pixel count')
xlabel('a value');
ylabel('b value');
[id,cl]=kmeans(ab,3);
figure(2);
clf;
hold on;
cm = paruly(3);
for i=1:3
vi = find(id==i);
plot(ab(vi,1),ab(vi,2),'+','Color',cm(i,:));
plot(cl(i,1),cl(i,2),'md','MarkerFaceColor','m');
end
xlabel('a value');
ylabel('b value');
set(gca,'YDir','reverse');
[r,c] = size(im_rgb(:,:,1));
im_cluster = reshape(id,r,c);
figure(3);
imagesc(im_cluster);
The end result is
Hmm, that was not what I was hoping for.
Compare with the original again.
It looks like the algorithm did a good job of finding the white lines but it didn't find the black dots I was looking for. Instead, it separated the red areas in the original picture into dark red and light red (maybe pink?) areas.
I have some ideas about how to improve the algorithm for this particular image (which I intend to address in future posts) but I think I've just demonstrated a general result of image processing. It's hard to find a single approach that works for every type of task. It's also hard to develop techniques that don't have a few fiddle factors (parameters that you adjust until 'something works').
Image processing is never easy but as you gain experience and learn more about the techniques that are available, you begin to make faster progress.
Next up, some thoughts on t-tests.